|
||||
|
|
|
||
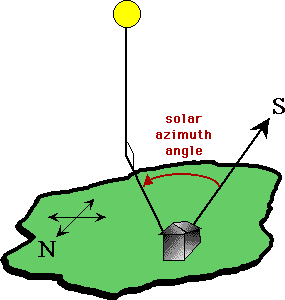
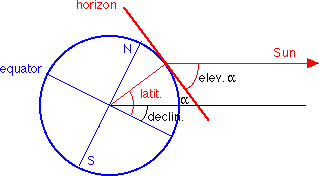
The solar azimuth angle is the angular distance between due South (see note below) and the projection of the line of sight to the sun on the ground. A positive solar azimuth angle indicates a position East of South, and a negative azimuth angle indicates West of South.
The azimuth angle is calculated as follows:
cos (Az) = (sin (Al) * sin (L) - sin (D)) / (cos (Al) * cos (L))
where:
Az = Solar azimuth angle
Al = Solar altitude angle
L = Latitude (negative for Southern Hemisphere)
D = Declination (negative for Southern Hemisphere)
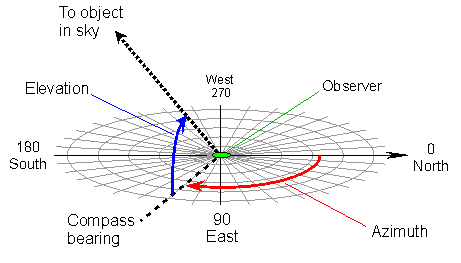
The
azimuth and
elevation angle are the coordinates of the observer's local
horizontal system:
the azimuth is the angular distance measured along the horizon (in
nautics 0°=N, 90°= E,
180°=S, 270°= W), the elevation is the angular distance measured above the
horizon.
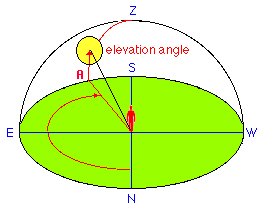
For a location of latitude beta the elevation angle of the sun at local noon is:
elev. angle = 90° - beta + declin
where declin is the declination angle of the sun.
Example: beta= 50° North
delta=23.5° on June 21:
elev. angle = 90° - 50° + 23.5° = 63.5°
delta=-23.5° on Dec. 21:
elev. angle = 90° - 50° - 23.5° = 16.5°
Setting the Viewpoint with Azimuth and Elevation
MATLAB enables you to control the orientation of the graphics displayed in an axes. You can specify the viewpoint, view target, orientation, and extent of the view displayed in a figure window. These viewing characteristics are controlled by a set of graphics properties. You can specify values for these properties directly or you can use the view command and rely on MATLAB automatic property selection to define a reasonable view.
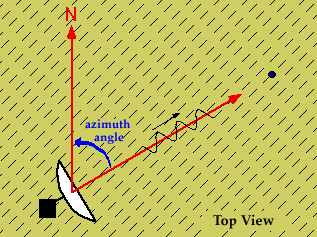
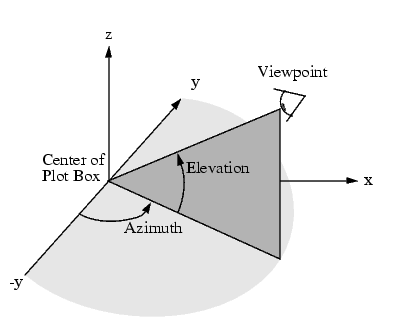
Azimuth and Elevation
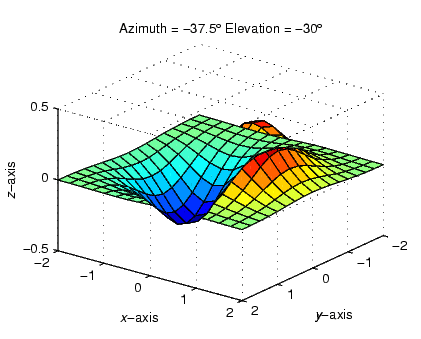
The view command specifies the viewpoint by defining azimuth and elevation with respect to the axis origin. Azimuth is a polar angle in the x-y plane, with positive angles indicating counterclockwise rotation of the viewpoint. Elevation is the angle above (positive angle) or below (negative angle) the x-y plane.
This diagram illustrates the coordinate system. The arrows indicate positive directions.
Default 2-D and 3-D Views
MATLAB automatically selects a viewpoint that is determined by whether the plot is 2-D or 3-D:
- For 2-D plots, the default is azimuth = 0° and elevation = 90°.
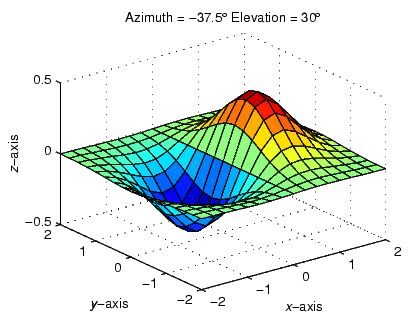
- For 3-D plots, the default is azimuth = -37.5° and elevation = 30°.
Examples of Views Specified with Azimuth and Elevation
For example, these statements create a 3-D surface plot and display it in the default 3-D view.
· [X,Y] = meshgrid([-2:.25:2]);
· Z = X.*exp(-X.^2 -Y.^2);
· surf(X,Y,Z)
·
·
·
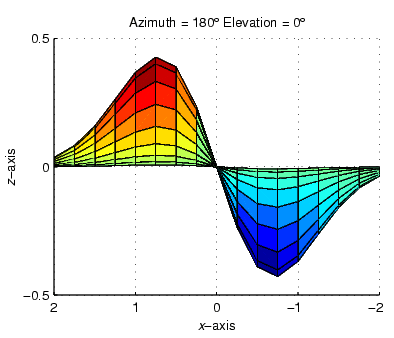
The statement
· view([180 0])
sets the viewpoint so you are looking in the negative y-direction with your eye at the z = 0 elevation.
You can move the viewpoint to a location below the axis origin using a negative elevation.
· view([-37.5 -30])
·
·
·
Limitations of Azimuth and Elevation
Specifying the viewpoint in terms of azimuth and elevation is conceptually simple, but it has limitations. It does not allow you to specify the actual position of the viewpoint, just its direction, and the z-axis is always pointing up. It does not allow you to zoom in and out on the scene or perform arbitrary rotations and translations.
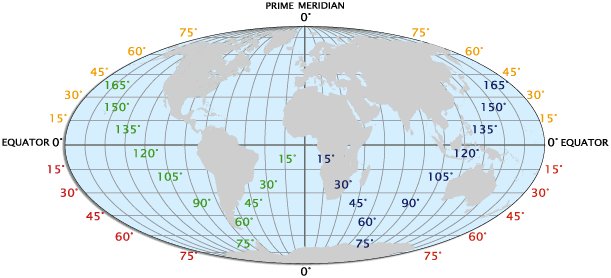
Green= degrees west longitude
Blue= degrees east longitude
Gold= degrees north latitude
Red= degrees south latitude
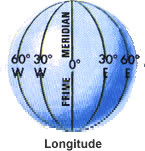
Latitude and longitude are imaginary lines dividing the earth into a grid in
order to identify any location on the earth's surface using coordinates.
Where the lines intersect, that spot is designated as (latitude, longitude)
in degrees. Longitude runs north/south and latitude runs east/west but
latitude is expressed as degrees north or south while longitude is expressed
as degrees east or west. For example Los Angeles, California is 34N, 118W.